CALCUL DANS UN REPERE

Après avoir compris la représentation d'un repère, la mise en place de points et de ses coordonnées, on va me demander d'effectuer des calculs, chaque fois bien entendu, vérifiables sur le dessin.

Comme je vous l'ai dit dans la fiche concernant les coordonnées de points, l'ensemble de ces calculs est basé sur les coordonnées x et y des points concernés : comme tout calcul, leur utilisation est très simple : il suffit seulement d'apprendre des formules........ Alors on y va ........

Les calculs que je peux faire avec des coordonnées de points :

Calcul de la distance entre 2 points

Si je veux (ou on me demande) par exemple de calculer la mesure du segment formé par 2 points du repère.

La formule de calcul de distance entre 2 points à savoir par coeur :

Pour une distance AB donnée on a :

Interprétation de la formule :

Cette formule a l'air très complexe, mais pas tant que ça : dictons la avec nos mots à nous :
"Une distance entre 2 points se calcule en faisant les différences respectives des x et y de chacun des deux points du segment pris en compte dans le calcul : ces 2 différences sont ensuite élevées au carré, puis additionnées entre elles : la distance effective s'obtient par la racine carrée du résultat de cette addition". Simple non ??

La règle : on soustraira toujours les coordonnée du point, origine du segment, à celles du point , extrêmité du segment

Application

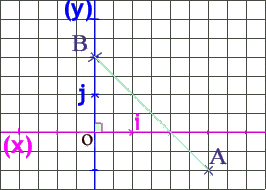
Dans un repère orthonormé O, I, J, de norme 1 cm, on donne : A ( 3 ; -1) et B ( 0 ; 2)

Tracer la figure correspondante
Calculer AB

1. Je trace mon repère et place mes points A et B conformément à leurs coordonnées comme vu dans la fiche N° 1.

 

2. Pour calculer AB, j'applique bêtement la formule que je viens d'apprendre par coeur :


AB =

Je regarde mes coordonnées de points :

A ( 3 ; -1) cela signifie que x_A = 3 et y_A = -1

B ( 0 ; 2) cela signifie que x_B = 0 et y_B = 2

Je peux maintenant remplacer les termes de ma formule par leur valeur :

AB =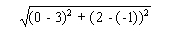

Je vais effectuer le calcul de mon expression :

(0 -3)² = (-3)² = 9
(2 - (-1))² = (2 + 1)² = 3² = 9
9 + 9 = 18

AB = 18
AB = 4,24 cm

Je peux vérifier cette longueur de segment avec ma règle sur le dessin.

Calcul des coordonnées du milieu d'un segment

Si on me demande de le faire, ou si je veux (ou on me demande) de montrer qu'un point est milieu d'un segment.

Pour un segment AB donné, le milieu I de ce segment aura pour coordonnées : I (; )

Interprétation de la formule :

Cette formule est tout de même plus simple que la 1ère non ? Elle signifie que les coordonnées du milieu d'un segment correspondent à (la moitié) des sommes respectives des x et y de chacun des deux points du segment.

Application

Reprenons le même repère orthonormé O, I, J, que ci-dessus et les mêmes points: A ( 3 ; -1) et B ( 0 ; 2)

Tracer la figure correspondante
Déterminer par le calcul les coordonnées de I, milieu du segment AB. Puis placer le sur le dessin


1. Je trace mon repère et place mes points A et B conformément à ci-dessus :

2. Pour calculer les coordonnées de I, milieu du segment AB , j'applique bêtement la formule que je viens d'apprendre par coeur :

I (; )

Je regarde mes coordonnées de points :

A ( 3 ; -1) cela signifie que x_A = 3 et y_A = -1

B ( 0 ; 2) cela signifie que x_B = 0 et y_B = 2

Je peux maintenant remplacer les termes de ma formule par leur valeur :

I ( )

Je vais effectuer le calcul de mon expression :

= = 1,5
= = 0,5

I (1,5 ; 0,5)

Je place mon point I sur le dessin, comme demandé. Bien entendu, je vérifie la cohérence de mon placement :

On aurait pu également me donner comme énoncé :

Le même repère orthonormé O, I, J, que ci-dessus et 3 points: les 2 mêmes A ( 3 ; -1) et B ( 0 ; 2) + un point I ( 1,5 ; 0,5)

Tracer la figure correspondante
Montrer que I est le milieu du segment AB


1. Je trace la figure (celle de ci-dessus)

2. Pour montrer que I est le milieu du segment AB, il me suffit de montrer que ce point possède les mêmes coordonnées que le milieu de ce segment, conformément au calcul des coordonnées du milieu d'un segment que je viens d'éffectuer :

Le milieu de AB a pour coordonnées (on pourrait le nommer M) :

M ()
M ( )
= = 1,5
= = 0,5

M (1,5 ; 0,5)

M a les mêmes coordonnées que I M = I ; Donc I milieu de AB

Calcul des coordonnées d'un vecteur

Ah ces fameux vecteurs - les pauvres, ils ne sont les amis de personne : c'est dommage, car leur concept n'est pas plus compliqué qu'un autre. Nous avons déjà abordé le sujet dans le chapitre sur les transformations : oui, rappelez-vous le vecteur est l'acteur principal de la translation.

Et bien dans un repère, un vecteur, c'est la même chose :

Il est représenté par 2 points qui délimitent sa mesure. Comme toujours, il a un sens, celui de sa flèche et une direction (c'est sa pente) (souvenez-vous : voir fiche)

Dans un repère, il aura en plus des coordonnées : et oui, comme un point : même principe : une valeur en x et une valeur en y : comme pour un point les coordonnées du vecteur peuvent se lire sur le dessin, mais surtout se calculent : c'est la manière la plus sûre d'obtenir des coordonnées exactes. La lecture sur le dessin sert souvent de vérification du calcul.


La formule de calcul des coordonnées d'un vecteur :

Pour deux points AB donnés , les coordonnées du vecteur formé par ces points sont égales à : (xB - xA ; y B - yA)

Interprétation de la formule :

Les formules sont de plus en plus simples, n'est-ce pas ? Cette formule revient à faire la soustraction respectives des x et y de chacun des deux points formant le vecteur : "Soustraction des coordonnées du point origine du vecteur de celles du point "destination" du vecteur (c'est le sens du vecteur exprimé par la flèche)"

Ici, on va bien de A vers B, donc on soustrait les coordonnées de A à celle de B ; si on était allé de B vers A, on aurait eu alors un vecteur .(opposé d'ailleurs au vecteur ) - les coordonnées de ce vecteurs auraient donc été obtenues par la soustraction des coordonnées de B à celles de A : simple non ??

Application

Même repère que d'habitude - Mêmes points A et B avec A ( 3 ; -1) et B ( 0 ; 2)

Tracer la figure correspondante
Calculer les coordonnées du vecteur puis vérifier ses coordonnées sur le dessin; calculer ensuite les coordonnées du vecteur . Que remarque-t-on ?


1. Je trace mon repère et place mes points A et B conformément à ci-dessus :

Je n'oublie pas cette fois-ci, puisque je parle de vecteur, de représenter la flèche qui indiquera son sens : ici, vecteur : sens : de A vers B (bas en haut)

2. Pour calculer les coordonnées de , il me suffit d'appliquer bêtement la formule que je viens d'apprendre par coeur :

(x_B - x_A ; y _B - y_A)

Je regarde mes coordonnées de points :

A ( 3 ; -1) cela signifie que x_A = 3 et y_A = -1

B ( 0 ; 2) cela signifie que x_B = 0 et y_B = 2

Je peux maintenant remplacer les termes de ma formule par leur valeur :

(0 - 3 ; 2 - (-1))

Je vais effectuer le calcul de mon expression :

0 - 3 = -3
2 - (-1) = 2 + 1 = 3

(-3 ; 3)

Comme demandé, je vais maintenant vérifier que les coordonnées du vecteur que je viens de calculer sont exactes :


Méthode : Pour vérifier les coordonnées de mon vecteur, je regarde le "chemin" que je dois parcourir sur mon dessin pour me rendre du point A au point B : le "chemin" réalisé à l'horizontale correspondra au x de mon vecteur, le "chemin" parcouru à la verticale sera le y de mon vecteur :

Une règle très importante de lecture :

• si je recule pour x ,ou descend pour y par rapport à mon point de départ, ma coordonnée sera négative
  
• si j'avance pour x ,ou monte pour y par rapport à mon point de départ, ma coordonnée sera positive

Lecture des coordonnées de :


Pour aller de mon point A à mon point B je :


• Recule de 3 graduations à l'horizontale
• Monte de 3 graduations à la verticale


Conformément à ce que je viens de voir, cela signifie que :

• xsera négatif puisque je recule à l'horizontale
• y sera positif puisque je monte à la verticale
  
  
• x sera négatif de 3, puisque je recule de 3 graduations à l'horizontale
• y sera positif de 3, puisque je monte de 3 graduations à la verticale
  

Résultat : coordonnées de par lecture graphique : (-3 ; 3)

Mon calcul vient d'être vérifié par la lecture ; je suis donc sûre que mon résultat est correct (à moins de m'être trompée les 2 fois)


3. Calculons maintenant les coordonnées de , selon la même méthode :

(x_A - x_B ; y _A - y_B)

Je regarde mes coordonnées de points :

A ( 3 ; -1) cela signifie que x_A = 3 et y_A = -1

B ( 0 ; 2) cela signifie que x_B = 0 et y_B = 2

Comme tout à l'heure, Je peux maintenant remplacer les termes de ma formule par leur valeur :

(3 - 0 ; (-1) - 2)

J'effectue le calcul de mon expression :

3 - 0 = 3
(-1) - 2 = -3

Mon vecteur a pour coordonnées (3 ; - 3)

Qu'est-ce que je remarque ? que les coordonnées du vecteur sont l'opposé des coordonnés du vecteur . logique me direz-vous, puisque les 2 vecteurs sont opposés :
cette remarque entraîne donc une propriété que je dois connaître :



Si deux vecteurs sont opposés, alors leurs coordonnées aussi sont opposés.





Calcul de l'égalité de deux vecteurs



C'est sans doute la partie la moins comprise par le plus grand nombre : elle n'a pourtant comme d'habitude, rien de très compliquée !!

Nous abordons ici le thème de l'égalité de 2 vecteurs déjà expliquée également dans le chapitre sur les translations

Ce que je sais déjà sur l'égalité de 2 vecteurs, pour l'avoir lu dans cette fiche :

2 vecteurs sont égaux si :

• Ils ont la même mesure
• Le même sens
• La même direction : cette propriété signifiant que 2 vecteurs égaux sont parallèles
  

Ce que je dois maintenant savoir sur l'égalité de 2 vecteurs dans un repère, et notamment pour le calcul des coordonnées d'un point :

 

Pourquoi ces propriétés sont-elles très importantes ?

Car très souvent, dans un exercice sur les repères, elles vont me servir :

Pour montrer que le quadrilatère formé par 4 points dont j'ai les coordonnées est un parallèlogramme

Pour calculer les coordonnées d'un point, qui sera l'un des 4 sommets d'un parallèlogramme

Application

Egalité de 2 vecteurs pour former un parallèlogramme :

Enoncé : Dans un repère orthonormé, on place les points suivants :
A(-1 ; 1) B (1 ; 0) C( 2 ;1 ) D (4 ; 0)

Tracer le repère et placer les points
Montrer par le calcul que le quadrilatère ABDC est un parallèlogramme


1. Je trace mon repère et place mes points A, B, C et D comme je sais si bien le faire maintenant :

Il semble bien que le quadrilatère formé par les 4 points ainsi placés soit un parallèlogramme.Il va me falloir maintenant le montrer par le calcul. Comment?

Et bien simplement en utilisant la propriété d'égalité de 2 vecteurs:

Si 2 vecteurs sont égaux, alors le quadrilatère formé par leurs 4 points est un parallèlogramme.

Et comment montrer que 2 vecteurs sont égaux ? Et bien simplement en utilsant la propriété d'égalité de2 vecteurs dans un repère:

"2 vecteurs sont égaux si leurs coordonnées sont égales."

Pour montrer que ABDC est un parallèlogramme, je vais donc regarder si les coordonnées du vecteursont égales à celles du vecteur .

Attention : je prends garde de comparer 2 vecteurs qui ont déjà le même sens,et apparemment la même direction (semblent parallèles) : j'aurais pu également comparer les coordonnées des vecteurs et ou encore les vecteurs et ou et: le principe aurait été exactement le même !!


Si l'égalité des coordonnées des 2 vecteurs est vérifiée, cela voudra dire que les 2 vecteurs sont égaux, et donc, que leurs 4 points forment un parallèlogramme.
Facile non ?

a. Je calcule les coordonnées du vecteur

(x_B - x_A ; y_B - y_A)
(1 - (-1) ; 0 - 1)
( 2 ; -1)


b. Je calcule les coordonnées du vecteur
(x_D - x_C ; y_D - y_C)
(4- 2 ; 0 - 1)
(2 ; - 1)

Youpii !!! Les coordonnées des 2 vecteurs sont bien égales ; je vais donc pouvoir écrire :

= , donc le quadrilatère ABDC est un parallèlogramme.

Et voilà : ma démonstration est terminée !

Remarque : j'aurais aussi pu avoir l'énoncé suivant :

Même repère et mêmes coordonnées de points à placer.

Tracer le repère et placer les points
Calculer les coordonnées de et . Que constate-t-on ? Que peut-on dire du quadrilatère ABDC ?


Après avoir calculé les coordonnées des 2 vecteurs par la même méthode, j'aurais conclue :
"Je constate que les vecteurs et sont égaux, car ils ont les mêmes coordonnées. Je peux donc dire que le quadrilatère ABDC est un parallèlogramme."


Egalité de 2 vecteurs pour trouver les coordonnées d'un point, 4è sommet d'un parallèlogramme

Enoncé : Dans un repère orthonormé, on place les points suivants :
A(-1 ; 1) B (1 ; 0) C( 2 ;1 )

Tracer le repère et placer les points
Calculer les coordonnées du point D pour que le quadrilatère ABCD soit un parallèlogramme. Placer le point D dans le repère


Le problème est posé inversement du précédent. Je vais donc me servir des mes propriétés d'égalité de 2 vecteurs, mais à l'envers.

1. Je trace mon repère et place mes 3 points A, B, et C

Je regarde : pour que le quadrilatère ABDC soit un parallèlogramme, il semblerait qu'il faille que le point D se situe au point de coordonnées (4 ; 0). Je vais devoir le vérifier par le calcul. Comment ? Et bien simplement en partant du fait que si le quadrilatère ABDC est un parallèlogramme, cela implique que = (ou = ; = ou encore =)

Et si = alors les coordonnées de sont égales à celles de : logique non ??

Je vais donc, comme tout à l'heure, calculer les coordonnées de et les coordonnées de

a. Coordonnées du vecteur

(x_B - x_A ; y_B - y_A)
(1 - (-1) ; 0 - 1)
( 2 ; -1)

b. Coordonnées du vecteur
(x_D - x_C ; y_D - y_C)


Et c'est là que le problème se pose : je ne connais pas les coordonnées du point D, puisque je les cherche. Par contre, comme je viens de l'expliquer, vu que ABCD doit être un parallèlogramme, doit être égal à, donc avoir les mêmes coordonnées.

Je peux donc dire =

Je sais que(2 ; - 1)

C'est grâce à cela que je vais pouvoir déterminer les coordonnées de mon point D.
Comment ?
Je peux écrire :

x= 2 = x_D - x_C = x_D - 2
y= - 1 = y_D - 1

DONC : 2 = x_D - 2 et - 1 = y_D - 1

Comme je résouds n'importe quelle équation, je vais extraire x_D et y_D

xD = 2 + 2 xD = 4

yD = - 1 + 1 yD = 0

Mon point D aura donc pour coordonnées (4 ; 0 )

Je le place comme demandé sur mon repère : le point D occupe bien la place que je lui avais prévue par la lecture : avec un point D de coordonnées (4 ; 0), le quadrilatère ABDC est bien un parallèlogramme

Et voilà le tour est joué ! Nous venons de voirl'ensemble des exercices demandés dans un repère.

ATTENTION : il existe également un chapitre très important gérant l'utilisation d'un repère, et de coordonnées de points : c'est celui des fonctions (affines et linéaires). Ce chapitre sera traité prochainement dans la partie activité numérique : une bonne raison de ne jamais perdre de vue la signification et l'utilisation de repères et de coordonnées de points, n'est-ce pas ??